Last Updated: May 3, 2025
First Law of Thermodynamics
Stated simply; The total energy of the universe does not change. This does not mean that the form of the energy cannot change. Indeed, chemical energies of a molecule can be converted to thermal, electrical or mechanical energies.
The internal energy of a system can change only by work or heat exchanges. From this the change in the free energy of a system can be shown by the following equation:
ΔE = q – w
When q is negative heat has flowed from the system and when q is positive heat has been absorbed by the system. Conversely when w is negative work has been done on the system by the surrounding and when positive, work has been done by the system on the surroundings.
In a reaction carried out at constant volume no work will be done on or by the system, only heat will be transferred from the system to the surroundings. The end result is that:
ΔE = q
When the same reaction is performed at constant pressure the reaction vessel will do work on the surroundings. In this case:
ΔE = q – w
where
w = PΔV
When the initial and final temperatures are essentially equal (e.g. in the case of biological systems):
ΔV = Δn[RT/P]
therefore,
w = ΔnRT
By rearrangement of the above equations one can calculate the amount of heat released under constant pressure:
q = ΔE + w = ΔE + PΔV = ΔE + ΔnRT
In this last equation, Δn is the change in moles of gas per mole of substance oxidized (or reacted), R is the gas constant and T is absolute temperature.
Enthalpy
Since all biological reactions take place at constant pressure and temperature the state function of reactions defined to account for the heat evolved (or absorbed) by a system is enthalpy given the symbol, H
The changes in enthalpy are related to changes in free energy by the following equation:
ΔH = ΔE + PΔV
The equation is written in this form because we are addressing the constant pressure situation. In the biological setting most all reaction occur in a large excess of fluid, therefore, essentially no gases are formed during the course of the reaction. This means that the value ΔV, is extremely small and thus the product PΔV is very small as well. The values ΔE and ΔH are very nearly equivalent in biological reactions.
Stated above was the fact that state functions, like ΔH and ΔE, do not depend on the path taken during a reaction. These functions pertain only to the differences between the initial and final states of a reaction. However, heat (q) and work (w) are not state functions and their values are affects by the pathway taken.
Reversible and Irreversible Reactions
In an idealized irreversible reaction such as one done by expanding an ideal gas against zero pressure, no work will be done by or on the system so the:
w = 0
In the case of an ideal gas (whose molecules do not interact) there will be no change in internal energy either so:
ΔE = 0
since ΔE = q – w, in this irreversible reaction q = 0 also.
In a reversible reaction involving an ideal gas, ΔE still will equal zero, however, the pressure will be changing continuously and work (w) is a function of P, work done must be determined over the entire course of the reaction. This result in the following mathematical reduction:
w = RTln[V2/V1]
Since in this situation ΔE = 0, q = w. This demonstrates that some of the heat of the surroundings has to be absorbed by the system in order to perform the work of changing the system volume.
Reversible reactions differ from irreversible in that the former always proceeds infinitely slowly through a series of intermediate steps in which the system is always in the equilibrium state. Whereas, in the irreversible reaction no equilibrium states are encountered. Irreversible reactions are also spontaneous or favorable processes. Thermodynamic calculations do not give information as to the rates of reaction only whether they are favorable or not.
Second Law of Thermodynamics: Entropy
The second law of thermodynamics states that the universe (i.e. all systems) tend to the greatest degree of randomization. This concept is defined by the term entropy, S.
S = klnW
where k = Boltzmann constant (the gas constant, R, divided by Avagadros’ number) and W = the number of substrates. For an isothermal reversible reaction the change in entropy can be reduced to the term:
ΔS = ΔH/T
Whereas, enthalpy is a term whose value is largely dependent upon electronic internal energies, entropy values are dependent upon translational, vibrational and rotational internal energies. Entropy also differs from enthalpy in that the values of enthalpy that indicate favored reactions are negative and the values of entropy are positive. Together the terms enthalpy and entropy demonstrate that a system tends toward the highest entropy and the lowest enthalpy.
In order to effectively evaluate the course (spontaneity or lack there of) of a reaction and taking into account both the first and second laws of thermodynamics, Josiah Gibbs defined the term, free energy which is defined as:
ΔG = ΔH – TΔS
Free energy is a valuable concept because it allows one to determine whether a reaction will proceed and allows one to calculate the equilibrium constant of the reaction which defines the extent to which a reaction can proceed. The discussion above indicated that a decrease in energy, a negative ΔH, and an increase in entropy, a positive ΔS, are indicative of favorable reactions. These terms would, therefore, make ΔG a negative value. Reactions with negative ΔG values are termed exergonic and those with positive ΔG values endergonic. However, when a system is at equilibrium:
ΔG = 0
Gibbs’ free energy calculations allows one to determine whether a given reaction will be thermodynamically favorable. The sign of ΔG states that a reaction as written or its reverse process is the favorable step. If ΔG is negative then the forward reaction is favored and vice versa for ΔG values that are calculated to be positive.
Standard State Conditions in Biological Reactions
To effectively interpret the course of a reaction in the presence of a mixture of components, such as in the cell, one needs to account for the free energies of the contributing components. This is accomplished by calculating total free energy which is comprised of the individual free energies. In order to carry out these calculations one needs to have a reference state from which to calculate free energies. This reference state, termed the standard state, is chosen to be the condition where each component in a reaction is at 1M. Standard state free energies are given the symbol: G°.
The partial molar free energy of any component of the reaction is related to the standard free energy by the following:
G = G° + RTln[X]
From this equation one can see that when the component X, or any other component, is at 1M the ln[1] term will become zero and:
G = G°
The utility of free energy calculations can be demonstrated in a consideration of the diffusion of a substance across a membrane. The calculation needs to take into account the changes in the concentration of the substance on either side of the membrane. This means that there will be a ΔG term for both chambers and, therefore, the total free energy change is the sum of the ΔG values for each chamber:
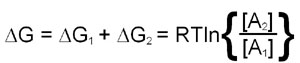
This last equation indicates that if [A]2 is less than [A]1 the value of ΔG will be negative and transfer from region 1 to 2 is favored. Conversely if [A]2 is greater than [A]1 ΔG will be positive and transfer from region 1 to 2 is not favorable, the reverse direction will be.
One can expand upon this theme when dealing with chemical reactions. It is apparent from the derivation of ΔG values for a given reaction that one can utilize this value to determine the equilibrium constant, Keq. As for the example above dealing with transport across a membrane, calculation of the total free energy of a reaction includes the free energies of the reactants and products:
ΔG = G(products) – G(reactants)
Since this calculation involves partial molar free energies the ΔG° terms of all the reactants and products are included. The end result of the reduction of all the terms in the equation is:
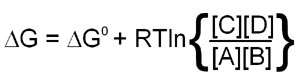
When the above equation is used for a reaction that is at equilibrium the concentration values of A, B, C and D will all be equilibrium concentrations and, therefore, will be equal to Keq. Also, when at equilibrium ΔG = 0 and therefore:
0 = ΔG° + RTlnKeq
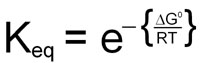
This demonstrates the relationship between the free energy values and the equilibrium constants for any reaction.
Coupled Reactions
Two or more reactions in a cell sometimes can be coupled so that thermodynamically unfavorable reactions and favorable reactions are combined to drive the overall process in the favorable direction. In this circumstance the overall free energy is the sum of individual free energies of each reaction. This process of coupling reactions is carried out at all levels within cells. The predominant form of coupling is the use of compounds with high energy to drive unfavorable reactions.
The predominant form of high energy compounds in the cell are those which contain phosphate. Hydrolysis of the phosphate group can yield free energies in the range of –2.4 kcal/mol to –14.8kcal/mol (–10 kJ/mol to –62 kJ/mol). The energy of reactions can be given in kcal/mol (the historical standard) or in the International System of Units (SI) standard which is kJoule/mole (kJ/mole). These two different energy values can be interchanged using the conversion factor where 1 kcal/mol = 4.2 kJ/mol. These molecules contain energy in the phosphate bonds due to:
- Resonance stabilization of the phosphate products
- Increased hydration of the products
- Electrostatic repulsion of the products
- Resonance stabilization of products
- Proton release in buffered solutions
The latter phenomenon indicates that the pH of the solution a reaction is performed in will influence the equilibrium of the reaction. To account for the fact that all cellular reactions take place in an aqueous environment and that the [H2O] and [H+] are essentially constant these terms in the free energy calculation have been incorporated into a free energy term identified as:
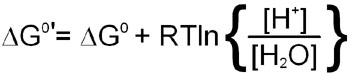
Incorporation of the last equation into a free energy calculation for any reaction in the cell yields:

Examples of Coupled Reactions in Biology
Let’s look at the hypothetical reaction: A → B. If this is a thermodynamically unfavorable reaction the ΔGo’ value will be positive. Let’s assume it is +4.0 kcal/mol. In order to drive this reaction in the direction written it can be coupled to the hydrolysis of ATP. The free energy of ATP hydrolysis to ADP is shown:
ATP + H2O → ADP + Pi: ΔGo’ = –7.3 kcal/mol
Coupling the two reactions together gives the equation:
A + ATP + H2O → B + ADP + Pi + H+
The ΔGo’ for this coupled reaction is the sum of the ΔGo’ values of the two separate reactions, i.e. (–7.3 kcal/mol) + (+4.0 kcal/mol) = –3.3 kcal/mol. This indicates that coupling ATP hydrolysis provides the energy necessary to make the conversion of A to B thermodynamically favorable.
Another useful example is to examine one of the reactions of glycolysis. In this case we will look at the oxidation of phosphoenolpyruvate to pyruvate catalyzed by the enzyme pyruvate kinase (PK):
phosphoenolpyruvate → pyruvate: ΔGo’ = –14.7 kcal/mol
This reaction releases sufficient energy to drive the synthesis of ATP from ADP and Pi which would normally be thermodynamically unfavorable with a ΔGo’ of +7.3 kcal/mol. Note that this value is the reciprocal of the hydrolysis of ATP. This points out another fact that the ΔGo’ for a reaction in one direction is equal but mathematically opposite for the reciprocal direction. Coupling the two reactions together yields:
phosphoenolpyruvate + ADP + H+ → pyruvate + ATP: ΔGo’ = –7.4 kcal/mol
